Mówi się, że matematyka opisuje rzeczywistość. Róg Gabriela jest obiektem pokazującym, że trzeba do tego stwierdzenia podchodzić z pewną dozą ostrożności i rozwagi.
O istnieniu w matematyce czyli aksjomat wyboru
Na początku XX wieku uwagę matematyków przykuł tzw. aksjomat wyboru, który przyprawił ich o niemały zawrót głowy i mocno podniósł kwestię tego co w matematyce wolno.
Kropki i słupki – prosty kombinatoryczny trik z rozmieszczaniem kul
Na ile sposobów można umieścić 10 nierozróżnialnych kul w 5 rozróżnialnych urnach? Okazuje się, że ten, i podobne problemy można rozwiązać używając prostego triku.
Punkt Fermata-Torricellego czyli ciekawy problem lokalizacji
Wyobraźmy sobie, że mamy trzy miejscowości i musimy wybrać lokalizację gazowni, która dostarczy do każdej z nich gaz. Jak to zrobić aby musieć zużyć jak najmniej rur na wybudowanie gazociągów do tych miejscowości? Problemy takiego
Jak Archimedes pole koła policzył
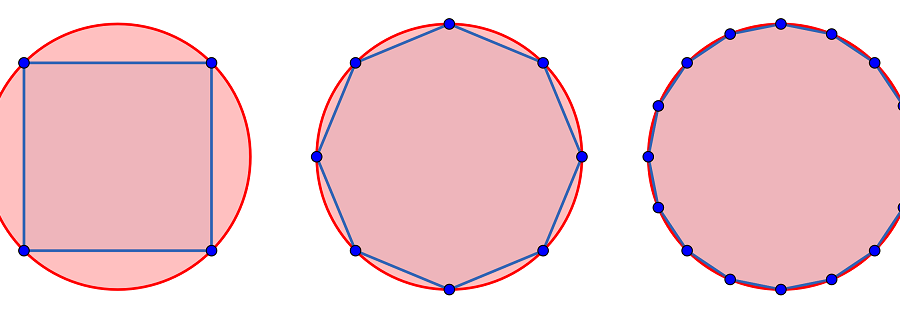
Wszyscy znamy ze szkoły wzór na pole koła. A czy wiemy skąd się wziął? Okazuje się, że pole koła policzyć umiał już Archimedes. Choć nie do końca jego wynik jest tym co znamy ze szkoły.
Paradoks Simpsona
Czy może się zdarzyć, że w każdej grupie wiekowej (wg jakiegoś podziału) pewna choroba występuje procentowo częściej u mężczyzn niż u kobiet, a jak się spojrzy na całą populację, to jest na odwrót, że występuje
Jak to się dzieje, że zbiór wszystkich zbiorów nie istnieje?
Mając dwa zbiory skończone z łatwością możemy stwierdzić, który z nich ma więcej elementów. Wystarczy policzyć. A czy można porównywać liczność zbiorów nieskończonych? Czy ma to w ogóle sens? W końcu nieskończoność to nieskończoność. A
Nie tylko okrąg! Parabola również ma swoje ,,pi”!
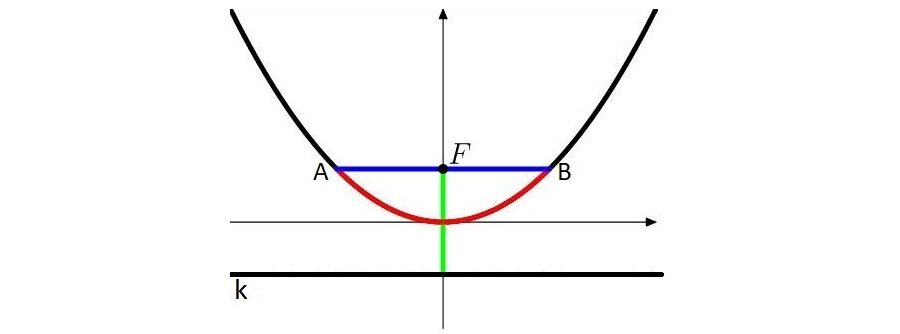
Wszyscy wiedzą, że stosunek obwodu okręgu do długości jego średnicy jest równy słynnej liczbie . Okazuje się, że parabola również ma swoje, nieco inne, , które będziemy nazywać (uniwersalną) stałą paraboliczną. Zacznijmy może od tego
Dlaczego 2 dodać 2 to jednak ZAWSZE 4 czyli czym jest działanie w matematyce?
Mówi się czasem, że 2 dodać 2 nie zawsze daje cztery. To oczywiście nieprawda gdy mówimy o matematyce, a dokładniej o dodawaniu liczb naturalnych, całkowitych itp., bo 2+2 zawsze jest równe cztery. Niemniej, jest to
Liczby przestępne i co o nich wiemy
Wiemy ze szkoły, że liczby rzeczywiste można podzielić na wymierne i niewymierne. Wśród tych drugich są tzn. liczby przestępne czyli takie jakby bardziej niewymierne. Mimo iż, co może niektórych zaskoczyć, prawie wszystkie liczby są przestępne,