Wszyscy znamy ze szkoły wzór na pole koła. A czy wiemy skąd się wziął? Okazuje się, że pole koła policzyć umiał już Archimedes. Choć nie do końca jego wynik jest tym co znamy ze szkoły. W tym wpisie przedstawimy zaadaptowany do dzisiejszych czasów dowód Archimedesa.
Mówiąc dokładniej, Archimedes nie do końca pokazał, że pole koła jest równe \(\pi r^2\). Pokazał natomiast, że jest ono równe polu trójkąta prostokątnego, którego jedna przyprostokątna ma długość \(r\), a druga jest równa obwodowi. Ponieważ obwód koła o promieniu \(r\) to \(2\pi r\), daje to znany nam wzór na pole \[P=\dfrac 12\cdot r\cdot 2\pi r=\pi r^2.\]
Mówienie nie o konkretnych liczbach, lecz o tym, że pole jednej figury jest równe polu innej było dosyć powszechne wśród starożytnych uczonych jak Archimedes.
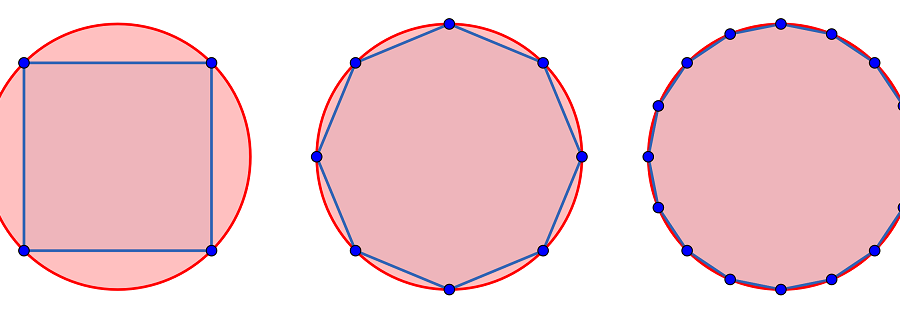
Idea dowodu Archimedesa była bardzo prosta. Polegała na przybliżaniu pola koła z dołu i z góry. Przybliżanie z dołu odbywa się poprzez wpisywanie w koło wielokątów foremnych o coraz większej liczbie boków 4, 8, 16,… . Przy czym, wpisujemy je tak, że każdy wierzchołek wielokąta o \(n\) bokach jest jednocześnie wierzchołkiem wielokąta o dwukrotnie większej liczbie boków.
Nowe wierzchołki następnego w kolejności wielokąta są środkami krótszych łuków okręgu łączących sąsiednie wierzchołki wyjściowego wielokąta. Wraz ze zwiększającą się liczbą boków, pole wielokąta zbliża się coraz bardziej do pola koła, jednak zawsze pozostaje od niego mniejsze.
Natomiast przybliżanie z góry odbywa się poprzez opisywanie na kole wielokątów foremnych, również o coraz większej liczbie boków 4, 8, 16, … .
Tym razem punkty styczności z okręgiem wielokąta o \(n\) bokach są również punktami styczności z okręgiem wielokąta o \(2n\) bokach. Tutaj także, punkty styczności z okręgiem następnego wielokąta powstają jako stosowne środki łuków. I naturalnie, gdy liczba boków się zwiększa, to pola wielokątów również coraz bardziej zbliżają do pola koła. Jednak, ponieważ to koło jest wpisane w wielokąty, to tym razem pole koła jest mniejsze od pola każdego wielokąta.
Swój dowód Archimedes zawarł w dziele O wymierzaniu koła. Chociaż powinniśmy się cofnąć do innego dzieła Archimedesa, tj. do pierwszej części O kuli i walcu, gdzie zawarte są założenia, z których Archimedes korzystał. Najpierw jednak przytoczymy dowód Archimedesa adoptując go do współczesnego języka. Potem zaś omówimy wspomniane aksjomaty oraz pewne wątpliwości, które mogą się pojawić czytając dowód. Ale do rzeczy.
Jeżeli pole \(P_K\) koła \(K\) jest różne od pola \(P_T\) wspomnianego trójkąta \(T\), to jest albo od niego większe albo mniejsze. Załóżmy na początek, że pole koła jest większe. Wówczas \[P_K-P_T = d\gt 0.\] Ważne jest, że podwajając liczbę boków wielokąta, różnica między polem koła a wielokąta zmniejsza się ponad dwukrotnie. Poniższy, pochodzący z dowodu twierdzenia 2 dwunastej księgi elementów, rysunek chyba jest dostatecznie przekonujący.
Sprawia to (co dopowiemy później), że dojdziemy w końcu do momentu gdy otrzymamy wielokąt \(W_n\), którego pole \(P_n\) będzie różniło się od pola koła o mniej niż \(d\). Pole owego wielokąta jest zatem większe niż \(P_T\). Łącząc środek koła z wierzchołkami \(W_n\) możemy podzielić wielokąt na przystające trójkąty równoramienne jak to pokazano poniżej.
Opuszczona ze środka koła wysokość \(h_w\) każdego z tych trójkątów jest krótsza niż promień koła, który ma taką samą długość jak jedna z przyprostokątnych trójkąta \(T\). Zauważmy jeszcze, że pole wielokąta \(W_n\) jest równe \[P_n = n\cdot\dfrac 12\cdot h_w\cdot a = \dfrac 12\cdot h_w\cdot Ob,\] gdzie \(Ob\) to obwód wielokąta. Obwód ten jest mniejszy od obwodu koła, który zarazem ma długość taką jak druga przyprostokątna trójkąta \(T\). Zatem pole wielokąta \(W_n\) jest mniejsze od \(P_T\) wbrew założeniu. Czyli pole koła nie może być większe od pola trójkąta \(T\).
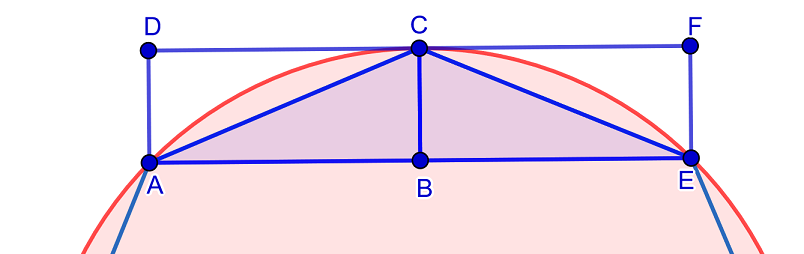
Teraz załóżmy, że pole koła jest mniejsze niż \(P_T\). W tej sytuacji \[P_T-P_K=d\gt 0.\] Do tego niech \(W_n\) będzie tym razem wielokątem foremnym opisanym na kole, a \(P_n\) jego polem. Pierwszą część dowodu przeprowadzimy, dla prostoty, dla kwadratu, ale można ją zastosować dla pozostałych wielokątów. Tak zresztą w zasadzie zrobił Archimedes. Załóżmy więc, że mamy na kole opisany kwadrat. Punkty styczności kwadratu z okręgiem dzielą okrąg na cztery łuki. Każdy z nich podzielmy na połowy otrzymując nowe punkty. Np. punkt \(D\) jest środkiem łuku \(\overset{\LARGE\frown}{FDE}\). Poprowadźmy styczne do okręgu przez te nowe punkty.
W tym momencie kluczową rzeczą jest pokazanie, że podwajając liczbę boków wielokąta opisanego, różnica \[d_n=P_n-P_K\] zmniejsza się ponad dwukrotnie, tj. \[d_{2n}\lt\dfrac{d_n}{2}\] Coś podobnego pojawiło się w pierwszej części dowodu. Pokażemy to później. Teraz zobaczmy w jaki sposób wykorzystał to Archimedes. Przy założeniu, że to prawda, podwajając liczbę boków opisanego wielokąta, prędzej czy później dojdziemy do momentu, gdy \(d_n\lt d\), tj. gdy pole wielokąta będzie większe od pola koła o mniej niż \(d\). W szczególności, pole wielokąta \(W_n\) będzie mniejsze niż pole trójkąta \(T\).
Ale zauważmy, że tak jak wcześniej, możemy wielokąt podzielić na trójkąty.
Poprowadzona ze środka koła wysokość każdego z tych trójkątów równa jest promieniowi. Teraz wystarczy zauważyć, że obwód wielokąta jest większy niż obwód koła bo przypomnijmy, że pole wielokąta jest równe \[P_n=\dfrac 12\cdot h_w\cdot Ob,\] gdzie \(Ob\) to jego obwód, a \(h_w\) to długość narysowanej wysokości. Co wobec tego, iż \(h_w=r\) daje nam, że \[P_n=\dfrac 12 \cdot r\cdot Ob.\] Z tego wynika, że pole wielokąta jest jednak większe od pola trójkąta bo, obwód wielokąta jest większy od obwodu koła, który z kolei ma taką samą długość jak dłuższa przyprostokątna trójkąta \(T\). Otrzymaliśmy znowu sprzeczność dowodzącą, że pole koła również nie może być mniejsze od pola trójkąta \(T\). Ostatecznie \[P_T=P_K\]
Oprócz pominiętych części jest jeszcze kilka rzeczy w przytoczonym dowodzie, które należy wyjaśnić, a które, co zrozumiałe, mogą wydawać się oczywiste. Zwłaszcza patrząc z perspektywy matematyki współczesnej. Czy aby na pewno Archimedes nie pominął jakichś szczegółów? Pamiętajmy, że w dowodzie Archimedesa próżno szukać wzmianek typu, że coś wynika z tego i tego twierdzenia. Mimo to Archimedes podchodził do sprawy dowodzenia nader poważnie. Jak zresztą i inni starożytni matematycy.
Kluczowe będzie to czy potrafił pokazać fakt, z którego korzystał niejawnie w dowodzie lub czy ewentualnie był on mu znany z innych źródeł. Mianowicie to, że z faktu iż \[d_{2n}\lt\dfrac{d_n}{2}\] wynika, że otrzymamy w końcu \(d_{k}\), które będzie dowolnie małe, będzie mniejsze od dowolnej liczby \(\epsilon\gt 0\). Nie wspominając o takich faktach, jak to, że np. obwód wielokąta opisanego jest większy niż obwód koła. Ale najpierw zajmijmy się pominiętymi częściami dowodu.
Na początek przypomnijmy rysunek.
Zauważmy, że \(|BD|=|BE|\) bo są one poprowadzone z \(B\) do punktów styczności z okręgiem. Do tego \[|BC|\gt |BD|=|BE|,\] bo \(|BC|\) to przeciwprostokątna, a więc najdłuższy bok, trójkąta \(\triangle BCD\). Do tego wysokość \(DG\) jest wspólną wysokością trójkątów \(\triangle BCD\) oraz \(\triangle BDE\).
Podsumowując, pole trójkąta \(\triangle BCD\) jest większe niż pole \(\triangle BDE\). Ze względu na symetrię, pole trójkąta \(\triangle ABC\) jest większe niż pole wielokąta będącego sumą trójkątów \(\triangle AFD\) oraz \(\triangle BDE\). A więc w szczególności jest większe od zaznaczonego poniżej na ciemnoniebiesko pola równego \(d_8\).
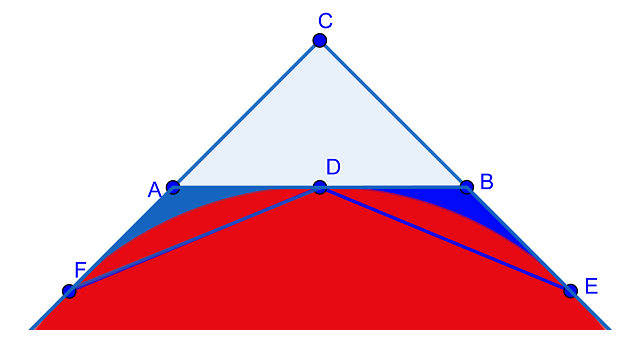
Zatem \[d_8\lt \dfrac{d_4}{2}.\] Powyższe rozumowanie można bez zmian przenieść na sytuację ogólną, gdy z wielokąta o \(2^k\) bokach przechodzimy do wielokąta o \(2^{k+1}\) bokach dla pewnego \(k\gt 1\). Tak mniej więcej wyglądał dowód Archimedesa, z którym można się zapoznać np. w tym miejscu. Jest to angielskie wydanie dzieł Archimedesa. Jest tam m.in. O wymierzaniu koła jak również O kuli i walcu. Polskiej wersji niestety nie udało mi się znaleźć.
Teraz trochę się cofnijmy do tego jakie w ogóle założenia przyjmował Archimedes. Na początku dzieła O kuli i walcu Archimedes umieścił pięć aksjomatów, które uznał za niewymagające dowodzenia. Taka praktyka nie była niczym nadzwyczajnym w starożytności. Wystarczy choćby wspomnieć aksjomaty Euklidesa. Za aksjomaty przyjmowano własności, które są na tyle oczywiste, że uznano iż nie trzeba ich udowadniać i korzystając z nich dowodzono dalszych własności i twierdzeń. W końcu od czegoś trzeba zawsze zacząć! Aksjomatyzacja jest w matematyce czymś powszechnym. Proces, w którym wyłuskujemy kluczowe własności z jakichś ważnych matematycznych obiektów by przyjąć je za wstęp do nowej definicji jest powszechny w matematyce. Przykładowo takie własności dodawania liczb całkowitych jak:
- łączność,
- własność zera, że \(0+n=n+0=n\),
- istnienie liczby przeciwnej
stały się podstawą definicji jednej z najważniejszych struktur algebraicznych, tj. grupy.
Ale wróćmy do Archimedesa. W kontekście pola koła będą nas interesowały dwa lub nawet trzy aksjomaty. Pierwszy z nich to:
- Ze wszystkich linii o tych samych końcach, odcinek jest najkrótszy.
Z kolei drugi aksjomat wymaga pewnego wyjaśnienia, gdyż pojawia się w nim pojęcie linii wypukłej. Jest to taka linia, która, mówiąc nieco niematematycznie wygina się (lub puchnie) w jedynym kierunku. Lub nieco inaczej czyli zasadniczo tak jak definiuje to Archimedes, jest to taka linia, że jeżeli weźmiemy dowolne dwa jej punkty to odcinek je łączący leży w całości po jednej stronie linii lub ewentualnie na samej linii, ale nigdy po obu stronach. Na potrzeby dowodu Archimedesa będą nas interesowały jedynie linie wypukłe do góry (ewentualnie odcinki).
Natomiast linia niewypukła ma wgłębienia.
Widać tu analogię do pojęcia zbioru wypukłego, tj. mającego tę własność, że wraz z każdymi swoimi dwoma punktami zawiera w sobie odcinek je łączący. Jeżeli końce linii wypukłej połączymy odcinkiem, to otrzymamy krzywą ograniczającą właśnie zbiór wypukły.
Natomiast gdy zrobimy to samo dla linii niewypukłej, to otrzymamy zbiór, który wypukły nie jest i, w którym znajdzie się para punktów o tej własności, że odcinek je łączący nie znajdzie się w całości wewnątrz otrzymanej krzywej.
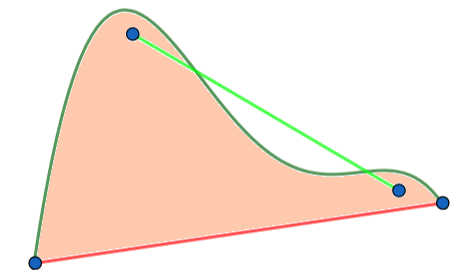
Ważnym przykładem linii wypukłej jest odcinek! Ale wróćmy do aksjomatów Archimedesa. Drugi z nich mówi, że jeżeli mamy dwie linie wypukłe łączące te same punkty, to ta wewnątrz jest krótsza.
Z tych dwu aksjomatów wynikają dwie bardzo ważne rzeczy, które wydają się oczywiste i można by rzec, że nie ma czego dowodzić. Ale to takie miejsce, w którym należy docenić matematyczną skrupulatność Archimedesa. Są założenia i z tych założeń dowodzimy reszty, nawet jeśli wydaje się to oczywiste. Podobnie jak w dzisiejszej matematyce. A wszystko to ponad 2200 lat temu!
Ale do rzeczy. Po pierwsze, jeżeli wielokąt foremny jest wpisany w okrąg, to jego obwód jest mniejszy od obwodu okręgu. Istotnie, każdy bok wielokąta wyznacza odpowiadający mu łuk okręgu o tych samych końcach. Więc pierwszy (a również i drugi) aksjomat mówi nam, że odcinek (czyli bok wielokąta) jest krótszy niż wspomniany łuk okręgu, który jest linią wypukłą. Spójrzmy na (oczywisty) rysunek.
Zaznaczono na zielono przykładowe boki wielokątów. Z tego już konkluzja oczywista. Obwód koła jest większy od obwodu wielokąta wpisanego w ten okrąg!
Po drugie, obwód wielokąta opisanego na okręgu jest większy niż długość samego okręgu. Co wynika z aksjomatu drugiego.
W obu pominiętych fragmentach korzystamy z faktu, że odejmując od pewnej wielkości (np. tą wielkością może być jakieś pole) sukcesywnie więcej niż połowę, otrzymamy w końcu wielkość mniejszą od innej zadanej. Fakt taki możemy znaleźć jako twierdzenie pierwsze X księgi Elementów Euklidesa. Ponadto warto tu przytoczyć kolejny aksjomat Archimedesa. Mówi on, że:
- Mając dwie różne wielkości, większa przewyższa mniejszą o taką wielkość, że kiedy dodawana do siebie, może być większa niż dowolna wielkość.
Innymi słowy nie istnieją wielkości nieskończenie małe. Nieważne jak małą liczbę weźmiemy (którą możemy utożsamiać np. z polem), to zwielokrotniając ją odpowiednią, skończoną ilość razy, otrzymamy liczbę dowolnie dużą. Odwracając rozumowanie, dzieląc daną wielkość przez odpowiednio dużą liczbę, otrzymamy wielkość mniejszą niż inna, dowolnie mała. Swoją drogą jest to znane jako aksjomat Archimedesa i leży u podstaw takich pojęć jak ciało archimedesowe. Ciekawe czy Archimedes by się spodziewał, że ok. dwa tysiące lat po jego śmierci jego imieniem nazywane będą pojęcia matematyczne. Na marginesie warto dodać, że to raczej nie Archimedes był autorem tego aksjomatu lecz Eudoksos.